Financial Planning: Asset Allocation

The concept of Modern Portfolio Selection is that an investor should know what return they need and then invest to get that return at the minimum risk possible. An underlying concept is that for a greater return you must accept greater risk. Higher yearly returns also mean higher yearly standard deviations in the value of your portfolio.

Achieving a greater return involves taking more risk, but you don't take any more risk than is necessary to achieve your target return.

(An excellent book on all this is The Intelligent Asset Allocator. I highly recommend it.)

For instance, if you need a return of 23% on your investments, you might have to accept a yearly standard deviation of 60%. That is, some years your portfolio will increase by 83% and some years your portfolio will decrease by 37%. You might be thinking, "Wow, if I can construct a portfolio that might yield 83%, why not just go for it?" Well, given the way random variables work, you might get 23% this year, or you might lose 37% of your portfolio value for many years before you get even one year of 83% return. Every year of 37% decrease will require a year of 83% return just to get you back to where you started. Can you afford to wait out the market? Given the way things go, you might have to delay your retirement for years. Taking this kind of risk when you don't need to is just foolish. (And if you need to take this kind of risk to make your plan work, then you need a different plan!)

If you are some kind of financial daredevil and your financial plan calls for a 35% annual return, you still don't want your portfolio to have any more risk than it has to. If there's an investment portfolio that yields 35% with a standard deviation of 60% why put your money into a portfolio that yields 35% with a standard deviation of 80%? That wouldn't be daredevil, that would just be stupid. (Stupid investors exit here.)

Modern Portfolio selection is based on the Markovitz model as detailed in the book Portfolio Selection. It's a gas of a read; kind of the Bible of investing, although it does not recommend a single investment. Instead it describes the science of investing. (p.s. It was written in 1957 and it is still the basis of financial investing.)

From earlier pages you know what return you need, now let's see how you construct a portfolio to get that return.

Asset Classes

An asset is something you own that is worth something. An investment is an asset you buy, hoping it will grow in value.

An investment opportunity is a chance you have to buy an asset. Mutual funds are investment opportunities, so are stocks, bonds, real estate, etc.

If we look at the historical performance of any asset, we can calculate it's average rate of return and it's standard deviation.

An asset class is a set of assets that have 1) the same average rate of return; 2) the same standard deviation; AND 3) their performance is closely correlated. Basically this means that an asset class is a group of investment opportunities that all behave the same. For instance, PG&E and SoCalElectric are probably in the same asset class. While they are two different companies, they are both subject to strong macro-economic effects: the price of oil, wars in the world, environmental legislation, etc. One might have had a hot management team for a while, the other might have had a failed power plant that had to be written off. Still, both are electric utilities, and over the years they have gone up and down in value about the same amount at about the same time. It makes sense. With only two investments in an asset class the standard deviation is probably pretty large. However, put 30 electric utilities into a group, throw out the five that are most loosely correlated with the others and soon you have a dependable asset class.

A computer program could (and does) look at all the history we have of all the investment opportunities and mathematically groups them into asset classes. I've read that the software in use today by professionals recognize about 150 asset classes.

Now that we have asset classes and know their historical performance the software calculates the coefficient of correlation between each and every asset class. For example, based on historical data, when class A goes up 10%, class B goes up 5%, class C goes down 3%, class D goes up 15%, etc., etc., etc. until the entire 150x150 matrix is filled in with all these correlations. It would look something like this:

Asset Class			Correlation
Name	Annual Return	Std Deviation	U	LC	TC	CP	ELC
Utilities (U)	5%	0.5	1	0.9	0.3	-0.8	-0.2
Large Capitalization Companies (LC)	20%	10		1	0.5	0.5	-0.7
Technology Companies (TC)	35%	45			1	-0.3	-0.1
Corp Bonds (CP)	8%	5				1	0.4
European Large Caps (ELC)	20%	15					1

The actual numbers above are just made up, but this understanding of the asset classes and their relative correlation is the basis of Modern Portfolio Selection. The performance of any one asset class is not predictable, but it does behave in an observed historical way against all the other asset classes under consideration.

Of course many investment opportunities don't fit into any class. Consider a mutual fund that has a "trade happy" manager. One day he's in technology stocks, the next month he's half into cash, the month after he follows a hot tip into undervalued utilities. Whew, he might have great returns but his mutual fund does not exhibit enough of a style to be grouped into an asset class. If this kind of market-timing investing is of interest to you, then when you invest your portfolio, keep some money out for the asset class called "wild rides" and do what ever you want. That money will not be part of the scientific approach we talk about here.

You may have heard of asset classes like "Large Capitalization Companies", "Utilities", etc. Mutual funds invest in assets and many of them have a stated profile to invest in a particular asset class. The mutual fund manager tries to pick the best-in-class companies. But mutual fund managers have a lot of leeway in the investments they make. For instance, an "International" mutual fund might buy big companies, little companies, utilities, financial institutions. A given mutual fund manager might even buy derivatives, bonds, or put a large chunk of money in cash. Portfolio management software, like Financial Engines, observes the behavior of a mutual fund and categorizes them by their actual investments rather than their stated strategy or their Morningstar classification. "Style Drift" is a measure that describes how much a fund manager changes the makeup of a fund over time. If you want to put some of your money into the asset class of "Utilities", then you want a Utilities mutual fund with very little Style Drift.

Portfolio Construction

Let's suppose you have $100 to invest and your financial plans call for a 20% return on your money. Let's also assume that you only have the four investment opportunities listed above. You might consider just putting all your money into the ELC asset class; it offers a historical return of 20% with a StdD of 10. However, the LC class offers the same historical return of 20% with less risk (lower StdD.). Why put your money in ELC if you could put it into LC? Clearly LC is the better investment choice.

Now, it might just be possible to construct a portfolio of the four asset classes above that offers the same 20% return of LC with an even smaller StdD - that is, even less risk. Why would a prudent investor take any more risk than necessary to achieve their targeted return? (Imprudent investors exit here.)

Suppose we do the math and find that putting $50 in LC, $20 in ELC, $10 in CB, and $20 in TC offers a 20% return with a StdD of 5? This investment mix would be a better portfolio than one which you put all $100 in LC. Note too that this portfolio includes a substantial investment (20%) in ELC. While a 100% ELC portfolio is not the best, the correlations between ELC and other asset classes makes it key to the new, better portfolio we just constructed.

Optimal (Efficient) Portfolios

I think you're now wondering, if a 50/20/10/20 portfolio returns 20% with a StdD of 5, is there some other allocation among these asset classes that would return 20% with even less risk? What about 40/10/30/20? What about 60/5/15/30? The possible mixes are infinite.

Different people have different financial objectives and make plans that require different rates of return. All prudent investors want to get the return they need at the minimum risk possible (Imprudent investors exit here). Since asset classes are universal, it would be great to know what the optimum portfolio mix is for each specific rate of return. If Joe needs 8% return, how would he allocate his assets among the 150 asset classes? If Sally needs 25% how would she allocate her assets among the 150 asset classes? Luckily for us, there is a computational solution to this optimization problem.

The efficient frontier is a curve that plots risk vs. return. The curve shows the minimum possible standard deviation that can be achieved for any given return. A portfolio which is on the curve is said to be "efficient." A portfolio that is not on the curve is inefficient because it is possible to allocate the assets differently to achieve the same return at a lower risk.

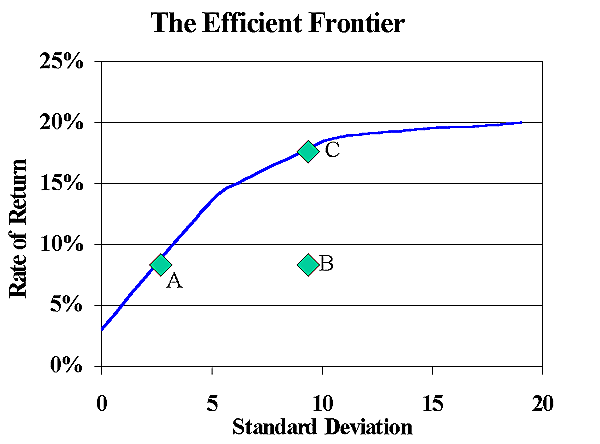An efficient frontier is shown in the example graph above. In this example the most efficient portfolio that would yield a 10% return would also have a standard deviation of 3.5. This is saying that no investment mix of the asset classes included in this particular model would yield 10% for any less risk than 3.5. Of course there are lots of asset allocations that would yield 10% return for a higher risk, but why would you do that?

 Consider portfolio B above. This is not an efficient portfolio because portfolio A yields the same return for much less risk. When I first started my financial planning thirty years ago my portfolio was positioned like B. I had a huge percentage of my assets in the stock of one company. The stock had done really well for a while, then cooled off, then done well, then cooled off. I came to realize that the science of investing left me only two choices: 1) if I was happy with the return I was getting, then I should diversify to reduce my risk, or 2) if I was comfortable with the amount of risk in my portfolio then I should dump it all into small cap funds and high yield junk bonds and get myself exposed to the returns of portfolio C. My portfolio B was just not a smart investment portfolio.

Having said all that, I was lucky enough to hook up with some friends who understood financial planning. They made me think of what my goals were and what return I really needed. They led me to understand that at the time neither portfolio A or C was right for me. At the time I needed a return of 11% to meet my financial goals and that required another portfolio somewhere between A and C. My friends had turned me into a precision investor.

Step 5: Next Steps